Il rilevamento della temperatura atmosferica

Centro per lo studio e la sperimentazione di strumentazione meteorologica

UTC Time

Sef Translate - joomla software for automatically website translationJoomla Translate

Confronto live dei sensori meteorologici installati presso il KWOS
Poggio Corese: Stazione meteorologica principale - Stazione meteo Ecowitt - Roma: Stazione meteo Meteohelix

Dettagli: Visite: 3634

Ripropongo un articolo scritto nel 2003.

Il rilevamento della temperatura con i termometri a resistenza ed il calcolo dell’errore nella misura, dovuto alla radiazione solare ( schermi attivi e passivi ).

Introduzione

In questa scheda ho cercato di focalizzare l’attenzione su quel tipo di termometri utilizzati spesso nelle stazioni meteorologiche automatiche degli amatori e professionisti: i termometri a resistenza.

Ho anche cercato di spiegare come la radiazione diretta sul sensore, possa influire sulla corretta misurazione della temperatura e quanto sia importante utilizzare la schermatura dello stesso.

La scheda è piuttosto tecnica ma già leggendola, senza soffermarsi troppo sulle formule, vi renderete conto di quanti e quali parametri entrano in gioco per effettuare una precisa misurazione della temperatura.

Il bilancio energetico

Il termometro, all’aria aperta, è avvolto da una corrente d’aria attraverso la quale effettua scambi di energia termica (convezione/conduzione e radiazione) e se l’aria è ricca di umidità, avvengono anche scambi termici di calore latente. Questi scambi di energia possono essere descritti da un bilancio energetico: la somma di tutte le energie ( Joule/sec ) deve essere uguale all’accumulo dell’energia termica all’interno del termometro.

Sorge spontanea una domanda: come calcoliamo l’energia accumulata all’interno del termometro? Ma ovviamte, con la sua temperatura !

Se consideriamo la temperatura all’interno del termometro come isoterma rispetto alla temperatura T, possiamo definire la capacità termica C (J/°K) e dire che per ogni variazione di temperatura DT, vi sarà uno scambio energetico C DT (J/°K).

Ora supponiamo che questa ipotetica variazione di temperatura all’interno del termometro sia avvenuta in un tempo relativamente piccolo ( °K/sec ) , possiamo definire la variazione della capacità termica nel tempo con C DT/Dt e saremo quindi in grado di scrivere la formula del bilancio energetico del termometro:

C DT/Dt = A ( Q* + Q_H + Q_E) + P

Dove A è la superficie del termometro. Q_{H e}Q_Esono le densità di scambio di calore conduttivo/convettivo e latente (unità, joule m.^-2 s^-1 = watt m.^-2 ), Q* è la densità della radiazione dello scambio di calore. P, infine, rappresenta la produzione di calore interna allo strumento, che possiamo supporre P=0 ma ricordiamoci che è un parametro importante nei sensori a termistore.

Ora supponiamo che il termometro sia immerso in una atmosfera asciutta e quindi si possano considerare nulli gli scambi di calore latenti e considerare solo gli scambi conduttivi/convettivi (Q_H).

Che formula matematica possiamo utilizzare per esprimere Q_H ? L’esperienza ci dice che il tasso di flusso di calore al/dal sensore dal/all’atmosfera circostante, dipende dalla differenza di temperatura dell’aria circostante con quella del termometro stesso (T_a- T). Possiamo considerare questa differenza come la forza che permette l’avvio dello scambio, ma non è tutto. Sappiamo che il calore non si scambia all’infinito ma vi è una certa resistenza. Certo è, che più veloce è il flusso dell’aria (vento), più veloce è lo scambio termico.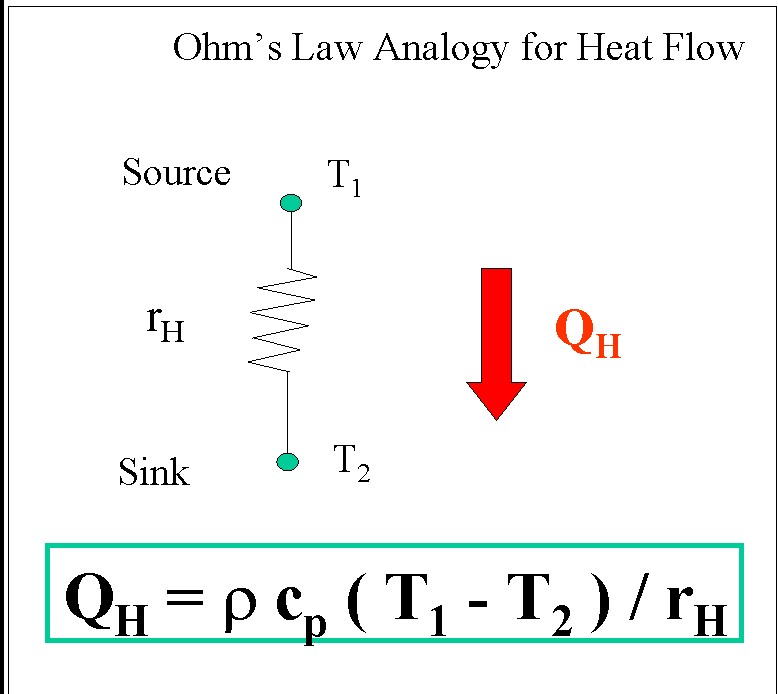

Possiamo quindi utilizzare una legge chiamata Analogia della Legge di Ohm:

Q_H = r_a c_pa (T_a-T)/r_H

Dove r_H è la “resistenza termica”, una funzione della velocità del vento (U) ed il fattore r_a c_pa(la densità dell’aria [ 1.1836 Kg/m³] e la capacità termica specifica dell’aria (calore specifico) [ 1004.6 J/Kg*°K] ) inserite per convenzione.

Questa legge viene chiamata Analogia della Legge di Ohm perché vi è una corrente di calore che si sposta tramite una differenza di temperatura e frenata da una resistenza.

Sostituendo ora l’espressione di Q_Hnella nostra equazione del bilancio energetico, avremo:

C DT/Dt = A r_a c_pa (T_a-T)/r_H(U)

Dove è necessario scrivere (T_a-T) per assicurare al termometro il tempo necessario per raggiungere la temperatura dell’aria che lo circonda. La notazione r_H(U) non significa che la resistenza termica deve essere moltiplicata per U, ma che dipende da U intesa come velocità del vento che incontra il termometro.

A proposito delle unità di misura, è facile intuire che la combinazione C r_H/(A r_a c_pa) dovrà avere una unità in formato temporale: questa è la costante di tempo del termometro. Ciò significa che dopo ogni cambiamento di temperatura dell’aria, vi sarà un ritardo di circa t=3t prima che l’equilibrio venga raggiunto. E quando il sensore è in equilibrio (quando DT/Dt=0) si avrà T= T_a .

Costante di tempo del termometro

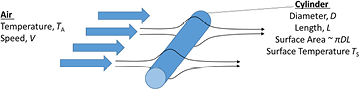thermistor diameter Quando calcoliamo delle variabili fisiche tenendo conto anche della costante di tempo, dobbiamo essere molto precisi. Assumiamo che il termometro abbia una forma cilindrica, di un raggio r e di una lunghezza l, e costituito di un materiale cha abbia una densità r ed una capacità di calore specifico c [J kg^-1 ^oK^-1]. Allora avremo C = r p r² l c , e A = 2p r l.

E quindi:

DT/Dt = (T_a-T)/ [r r c r_H/(2 r_a c_pa)]

Con un semplice calcolo, la costante di tempo sarà:

t = r r c r_H/(2 r_a c_pa)

Più grande sarà r, o più denso sarà r o maggiore sarà c del sensore, o minore sarà la velocità del vento, maggiore sarà la costante di tempo e quindi maggiore sarà il tempo per allineare la misura della temperatura alla reale temperatura dell’aria.

Tutto ciò è utilissimo per analizzare l’errore di radiazione ( errore nella misura della T_a ) dovuto ad un contributo non trascurabile della Q*.

Termometri a resistenza

Tipicamente la resistenza (R) di un conduttore metallico aumenta con il diminuire della sua temperatura. Si può quindi scrivere che:

R(T) = R(T_o) [1 + a (T-T_o) + b (T-T_o)² ]

Dove (T_o) è una temperature di riferimento e a e b sono specifici del conduttore.

Ecco la sensibilità alla temperatura a e il coefficiente high-order b, delle resistenze di alcuni termometri comunemente utilizzati:

	a [ 1/K ]	b [ 1/(K.K) ]
tungsteno	4.5e-3	0.5e-6
rame	4.3e-3	0
platino	3.92e-3	-0.55e-6
nichel	6.7e-3	?

Nota: se si considera una variazione di temperatura abbastanza stretta a partire da (T_o), il coefficiente b può essere considerato uguale a zero (b= 0).

Errore di radiazione proteggendo un sensore della temperatura in modalità aspirata e non.

I fotoni presenti nell’atmosfera sono classificati in due tipi: quelli di origine solare ( radiazione ad onda corta, fotoni con una lunghezza d’onda 0.3 µm <= l <= 4 µm) e quelli di origine terrestre ( radiazione ad onda lunga, fotoni con una lunghezza d’onda 4 <= l <= 100 µm). Possiamo così dividere la densità netta della radiazione Q* [W/m2] a/dal termometro in contributi a corta lunghezza d’onda (shortwave) e contributi a lunghezza d’onda più lunga (longwave):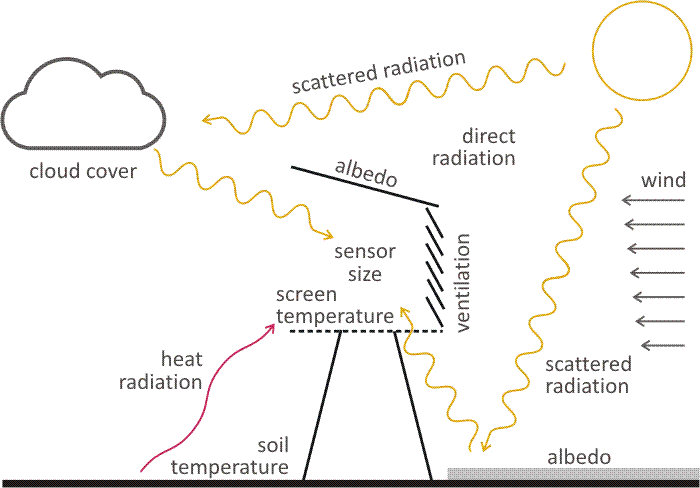 exposure

Q* = K* + L*

Dove K*=(1-r) K_inc, ed essendo K_inc la densità di flusso incidente (o verso il sensore), ed r la riflettività del corpo alle shortwave, si può assumere che in piena luce solare K_inc sia di circa 1000 W/m².

Allo stesso modo la densità netta del flusso delle longwave, è composto da una componente che va verso il sensore, ed una componente che parte dal sensore.

Secondo la legge di Stefan-Boltzmann noi sappiamo che il sensore della temperatura emette una densità di flusso: F = es T⁴

Dove e ≈ 1 è l’emissività e s=5.67x10^-8 [W m^-2 ^oK^-4] è la costante di Stefan-Boltzmann.

Esso riflette anche una frazione (1-e) di ogni radiazione incidente delle longwave L_inc, così la densità de flusso uscente diventa:

L_out = es T⁴ + (1- e) L_inc

Se il termometro è libero nell’aria (senza alcuno schermo intorno) e non vi è alcun impedimento all’arrivo dei fotoni provenienti da ogni direzione, sulla sua superficie, avremo una densità di flusso pari a: s T_gnd⁴ (T_gnd=temperatura del suolo).

La densità di flusso è determinata dall’emissione di vapore acqueo e CO₂nell’atmosfera, ma mentre la CO₂può ritenersi costante, il termometro è invece molto sensibile alle variazioni di temperatura ed umidità dell’aria.

A questo punto possiamo scrivere la formula relativa alle longwave se conosciamo le dimensioni e le specifiche tecniche del sensore, più la radiazione solare e la temperatura ambientale:

L* = s { T_env⁴ - T⁴ }

Dove T_env è la temperatura ambientale (quella interna ad un eventuale schermo) e T è la reale temperatura dell’aria.

E’ facile notare che se inseriamo il sensore all’interno di uno schermo solare, costruito così bene, da far diventare K_inc=0 ( in modo che non veda il sole ) e che la T_env ≈ T, allora Q*=0 !!

Uno schermo solare ben costruito, riduce drasticamente Q*, una buona aspirazione o ventilazione, inoltre, riducono ogni errore di radiazione residua.

L’errore di radiazione si può determinare partendo da un bilancio energetico:

C dT/dt = 0 = A (Q_H+Q*)

Dove, adottando l’analogia della legge di Ohm, si ha:

Q* = r_a c_pa (T-T_a)/r_H(U).

Finalmente si può ricavare l’errore di radiazione:

T - T_a = r_H Q*/(r_a c_pa)

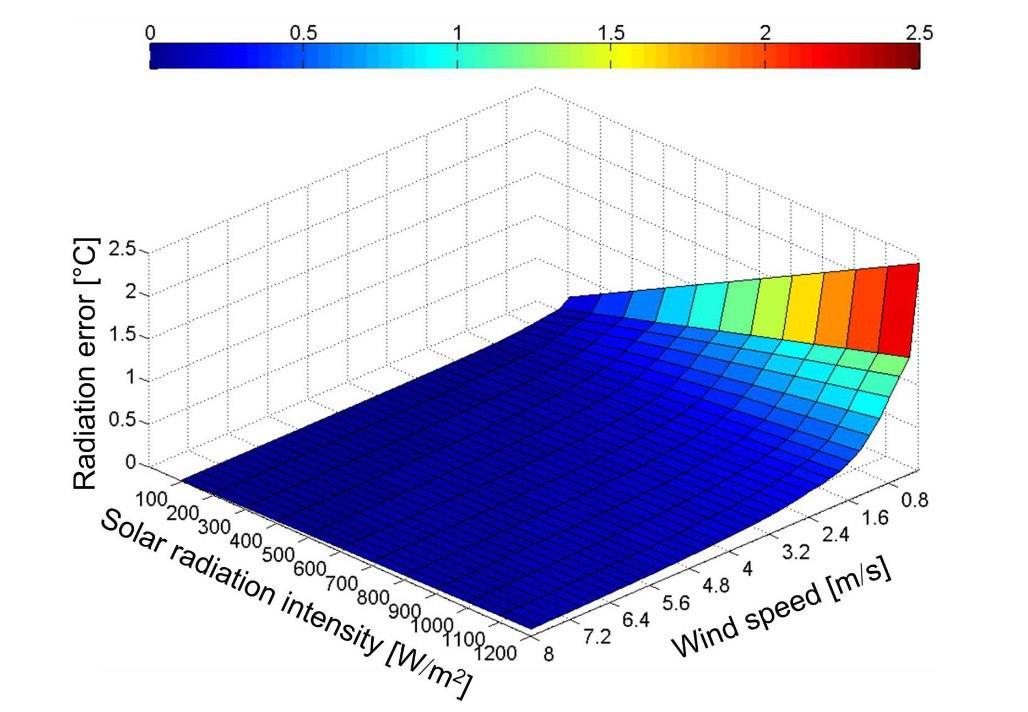
Si intuisce facilmente che poiché la resistenza termica è dipendente da U ( r_H(U) ) , l’errore di radiazione diminuisce con l’aumentare della velocità del vento.

La resistenza termica

La resistenza termica è, come abbiamo visto, un fattore che dipende dalla velocità del flusso d’aria che avvolge il nostro sensore, ma non è così semplice da calcolare, in quanto dipende anche dal suo spessore e dalla sua forma.

In maniera molto semplificata la resistenza termica si può esprimere in questo modo:

r_H = d/(D_H N_u)

dove d è lo spessore del sensore, D_Hè la diffusività termica dell’aria ed N_uè dato, approssimando per forme cilindriche dei sensori, dalla seguente regola:

R_e= ( U * d ) / ٧ se 0.1 < R_e < 10³ allora N_u= 0.32 + 0.51 R_e^0.52

con ٧ = viscosità cinematica dell’aria, U = velocità del vento e d = spessore termometro.

La viscosità cinematica e la diffusività termica dell’aria, dipendono dalla sua temperatura secondo la seguente tabella:

Temperatura	Viscosità cinematica	Diffusività termica
T	n	D_H
[C]	[m .m/s]	[m.m/s]
-5	1.29e-5	1.83e-5
0	1.33e-5	1.89e-5
5	1.37e-5	1.95e-5
10	1.42e-5	2.02e-5
15	1.46e-5	2.08e-5
20	1.51e-5	2.15e-5
25	1.55e-5	2.22e-5
30	1.60e-5	2.28e-5
35	1.64e-5	2.35e-5
40	1.69e-5	2.42e-5
45	1.74e-5	2.49e-5

Conclusioni

Abbiamo visto come calcolare l’errore di radiazione dovuto in particolar modo, ai fotoni provenienti dal sole nello spettro delle shortwave.

Se disponiamo di un piranometro (strumento per il rilevamento della radiazione solare), possiamo ora facilmente calcolare l’errore di radiazione di uno schermo entro il quale desideriamo inserire il nostro termometro.

Sappiamo infatti che l’errore di radiazione si calcola:

T - T_a = r_H Q*/(r_a c_pa)

Avremo quindi bisogno dei seguenti dati:

Velocità del vento che colpisce lo schermo di cui vogliamo conoscere l’errore di radiazione
Radiazione solare rilevata all’interno dello schermo ( quanto questo schermo protegge dalle shortwave ? )
Spessore del termometro ( preferibilmente di forma cilindrica per approssimare N_u)
Temperatura approssimata in cui effettuiamo la misurazione ( ammessi errori anche di 5°C )

Esempio:

Qual’ è l’errore di uno schermo solare sapendo che:

U (velocità del vento) = 3 m/s
Q* (radiazione solare all’interno dello schermo) = 65 W/m²D (spessore del termometro) = 15mm = 0.015 m
Temperatura approssimata, intorno a 35°C (per la scelta dei parametri ٧ e D_H ).

Calcoliamo subito i parametri necessari per trovare la resistenza termica :

La viscosità cinematica (٧) l’ho scelta nella tabella precedente sapendo che vi sono circa 35°C

R_e = (U * d) / ٧ = ( 3 * 0.015 ) / 0.000164 = 0.045 / 0.000164 = 274.39

Nu = 0.32 + 0.51 R_e^0.52= 0.32 + (0.51 * 274.39 ^0.52) = 0.32 + ( 0.51 * 18.53 ) = 0.32 + 9.45 = 9.77

E finalmente :

Anche la diffusività termica (D_H) è stata scelta dalla tabella precedente sapendo che vi sono circa 35°C

r_H= d/(D_H N_u) = 0.015 / ( 0.000235 * 9.77 ) = 0.015 / 0.0022 = 6.81

Ora non ci resta che sostituire tutto nella formula per il calcolo dell’errore di radiazione:

ricordiamoci che r_a e c_pa sono rispettivamente la densità dell’aria [ 1.1836 Kg/m³] e la capacità termica specifica dell’aria (calore specifico) [ 1004.6 J/Kg*°K]

T - T_a = r_H Q*/(r_a c_pa) = (6.81 * 65 )/ ( 1.1836 * 1004.6 ) = 442.65 / 1189.04 = 0.37°C